·密码学原理课程 —— Private-Key Cryptography Ⅰ
密码学原理专栏——非对称密码学,计算可证明安全,安全的基本定义,语义安全,构造EAV-Secure的加密方案
Private-Key (Symmetric) Cryptography
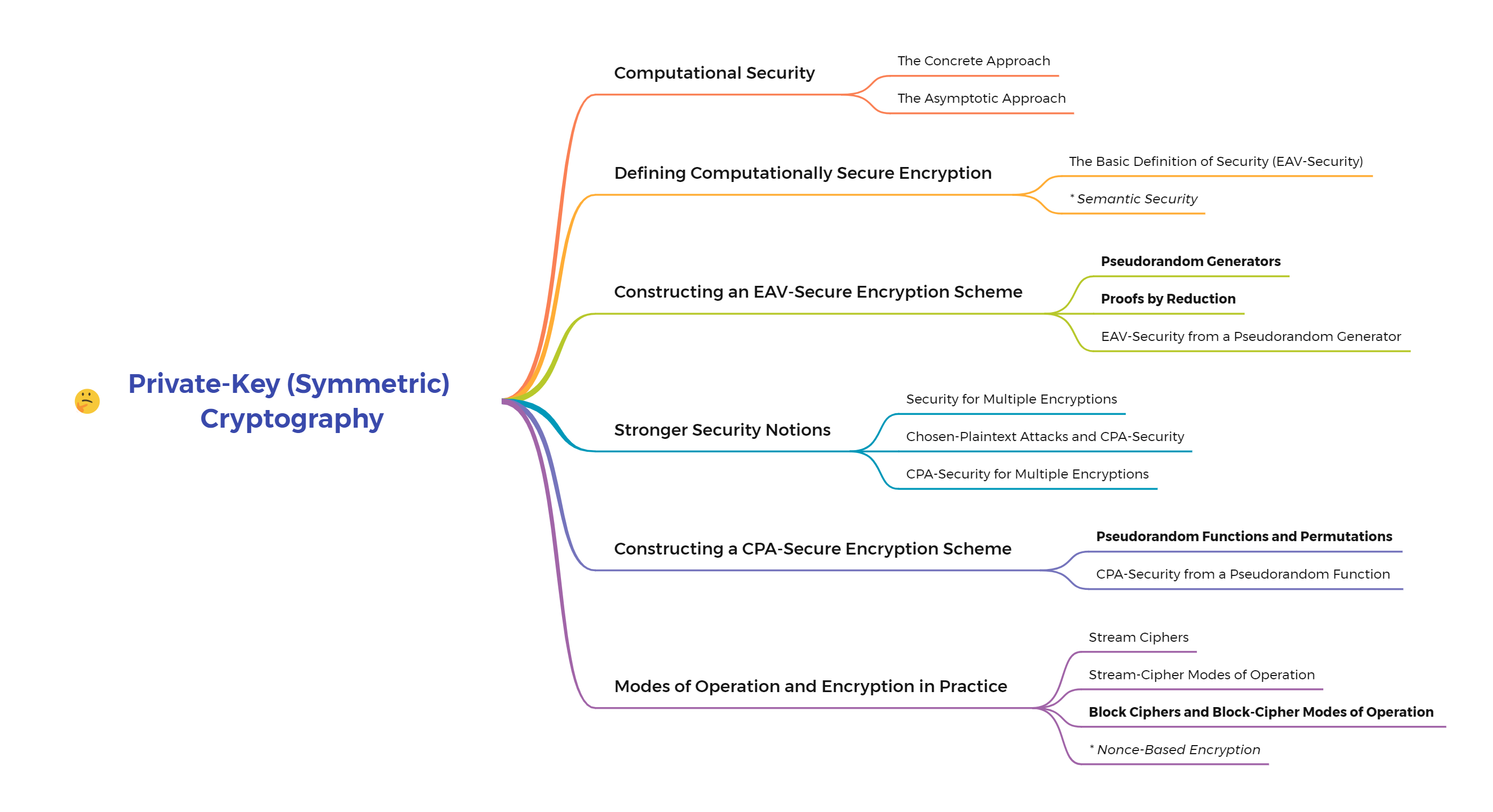
在本章节中,我们开始介绍两大密码学方向中的私钥/对称密码学(Private-Key/Symmetric Cryptography)方向。
(1)我们将会从弱化完善保密理论安全性开始,得到一个在实践生产中能够被接受并且符合实际人们对安全性需求的安全定义(computational secrecy)。
(2)接着我们从 computational secrecy 出发,给出一种最为基本的安全性定义—— EAV-Security(窃听者安全),并且对 Semantic Security 作出讨论。
(3)为了构造一个 EAV-Security Encryption Scheme 我们需要了解密码学中一个常用的组件—— Pseudorandom Generators,并且学习如何通过 Reductions 对一个 Encryption Scheme 的安全性作出证明。在上述铺垫过后,我们就可以构造一个 EAV-Security Encryption Scheme 并且使用 Reductions 去证明该方案的安全性。
(4)在实践应用中,密码方案仅达到 EAV-Security 是远远不足够的,这时候我们就需要一些安全性更强的定义(弱化对攻击者能力作出的限定而密码方案不被攻破),CPA-Security 与 CCA-Security 便是两种在安全性定义上更为严苛(攻击者的能力更加强大)的定义。
(5)有了上述定义过后,我们需要能够构造满足上述定义的加密方案。在构造具体的方案以前,我们需要介绍 Pseudorandom Functions and Permutations 两类定义,它们将在构造的具体方案中扮演重要的角色。
(6)最后,我们将会介绍在实践中使用的对称密码的两种形式—— Stream Cipher 和 Block Cipher,并介绍它们相应的操作模式。
Computational Security
完善保密理论为我们提供了信息论级别的安全强度,满足该理论定义的方案提供的安全性甚至不需要对攻击者的计算能力进行约束,是最为理想的情况(攻击者在观察到密文的情况下没有办法得到关于明文的任何一点信息),这也是我们加密的目的——为了保护明文中的信息。但完善保密理论的缺点也十分明显(我们在上一章节中有所讨论),而这些缺点在实际应用上是不可以接受的,我们需要对安全性作出妥协从而使得方案可落地执行并大面积推广使用。事实证明对完善保密理论进行弱化能够达到在保证足够安全性的同时在实践上也具有可操作性。我们只要假设 efficient attacker 在一个可被接受的时间跨度内密码方案被攻破的概率为一个可忽略的量即可,有关 「efficient」等概念我们将在后续的讨论中看到。
我们来看一个教材上有关于 Computational Security Encryption Scheme 的实例描述
一个加密方案需要窃听者在计算速度最快的计算机上投入至少200年的时间才能够以 $2^{-60}$ 这么小的概率能够获得密文泄露的明文信息,这时我们可以认为该加密方案是符合 Computational Secuirty 的。
通过对 Perfect Secrecy 安全性的弱化,我们得到了一个在实践上更具有意义的安全性表述。我们可以看到与 Computational Security 与 Perfect Secrecy 在下列定义中的区别,
- Security is only guaranteed against efficient adversaries that run for some feasible amount of time. 在这里我们能够发现,我们对攻击者的能力作出了限制,攻击者能够访问的计算资源有限并且其需要在规定的时间范围内攻破密码方案。如果我们的攻击者具有无约束的时间或计算能力,在此安全性定义下,它是能够攻破我们的密码方案的。不过在现实密码方案的构造中,我们可以通过精心设计密码方案使得任何一个现实意义上的攻击者都无法获得充足的资源(时间/计算)令其能够攻破该方案,这时候我们也可以认为该方案是牢不可破的。
- Adversaries can potentially succeed with some very small probability. 在该定义下,攻击者是有概率攻破满足 Computational Security 的方案的。不过我们能够使得该概率足够的小(就像我们上一个例子中的,小于 $2^{-60}$),这样我们也无需为一个小概率事件而担忧。(通常小概率事件的发生意味着系统本身的出现了设计者意料之外的事件,这些未被考虑的事件极大的影响了概率分布)
为了给 Computational Security 一个精确的定义,我们将会从以下两种路线来去描述 Computational Security.
The Concrete Approach
A scheme is $(t,\epsilon)-secure$ if any adversary running for time at most $t$ succeeds in breaking the scheme with probability at most $\epsilon$.
在 Concrete Approach 中,我们通过明确界定潜在攻击者成功攻破该密码方案的最大概率以及其在上面所投入的资源(时间/算力)总量去量化一个加密方案的安全性。在该定义中,攻击者能够使用的算力资源以及其能够花费的时间资源已经被限定,并且在上述限定之下攻击者的成功概率也仅为一个十分小概率 $\epsilon$,这样我们便给出了在 Concrete Approach 中 Computational Security 的定义。这种定义 Computation Security 的方法在实践中十分重要,因为它回答了使用密码方案的用户最为关心的问题(这个密码方案所承诺的安全性能够达到我的安全性需求吗?),并且给出了精确的表述。不过在有些情况下给出精确的量化表述是困难的,这时候我们就需要使用到另外一种 Computational Security 的定义方法。
The Asymptotic Approach
A scheme is computationally secure if any PPT(probabilistic polynomial-time) adversary succeeds in breaking the scheme with at most negligible(smaller than any inverse polynomial in n) probability.
由上述定义可以发现,这种渐进表述减少了对精确定量描述的使用。比如,在对攻击者能力进行限定时,该定义将攻击者能力抽象表述为具有概率多项式时间(PPT 攻击者在多项式时间内运行其攻击算法,其最多为 $p(n)$,取决于具体安全参数的大小)的攻击者,而不同于在 Concrete Approach 中 $(t,\epsilon)-secure$ 精确定义了攻击者能够使用的算力/时间资源。类似的,在表述攻击者在限制下成功攻破方案的概率时也使用了类似的抽象描述(negligible probability)而不是一个确切的概率值。这种不使用确切的量对 Computational Security 进行定义简化了抽象表述一个密码方案时步骤(我们在实践应用中仍然需要考虑 Concrete Approach),不过这也带来了一些需要解决的问题,我们需要准确地定义这些提到的抽象概念,使得在这种表述下的定义满足 Computational Security.
这种 Asymptotic Approach 根植于计算复杂度理论(回忆一下大 $O$ 记号),并且引入了安全参数 $n$ 用以观察在 $n$ 不断增长的情况下,参与到密码方案的主体(受信主体与攻击者)在计算上所花费时间的增长趋势。我们也可以认为这引入的安全参数 $n$ 与密钥的长度呈正相关、看作与攻击者攻击密码方案成功所需的运行时长相关、与攻击者成功攻击密码方案的概率相关等……事实上我们可以看到,随着安全参数 $n$ 的增加,密码方案是更加“安全的”(这种安全并不是由替换具体的密码方案带来的,而是通过增加密钥空间的大小来去降低攻击者进行 Brute-force Attack 成功的概率)。我们也会看到任意选取安全参数 $n$ 可能会给密码方案带来不一样的安全性,较小的 $n$ 可能毫无安全性可言,随着 $n$ 的增加不同的加密方案接近我们理想的安全需求的速率也不一样,这也是该方法称为 Asymptotic 的一个理由之一。值得注意的是,一个密码方案在实践中可用意味着合法可信的主体在使用该密码方案进行加密时其也运行着一个多项式时间的算法,并且该算法的时间复杂度要明确小于攻击者在缺少密钥信息的情况下所使用的攻击算法。这样以后即使在算力不断提升的情况下,我们仅需选用更大的安全参数 $n$ 来保障密码方案的安全性而不需要替换掉原有的密码方案,并且这对攻击者而言更加不利(在计算上的投入会比原先的更加大哪怕算力已经得到增长,这是由于其攻击算法的计算复杂度高于合法可信主体所带来的)。具体的例子可以参考教材(PG.46)
下面我们更进一步的讨论何为 negligible probability
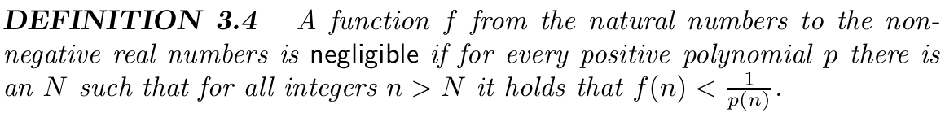
上述定义换一个表述有,对于所有的常数 $c$ ,存在一个整数 $N$ 使得对于所有的 $n>N$ 都有该式成立 $f(n)<n^{-c}$,熟悉高等数学的同学可以想象一下在高数中对于极限的定义。 不严谨的来说 $n^{c}$ 遍历所有的 $c$ 即得到了上述定义中所提到的 every positive polynomial p,并且注意到上述定义是对所有满足 $n>N$ 的整数,都有 $f(n)<\frac{1}{p(n)}$,替换一下就可以得到 $f(n)<n^{-c}$ . 具体例子可以在教材(PG.48)中得到。
negligible function 有一些很好的性质,下面我们就来看看它的这些性质以及这些性质的具体运用,!
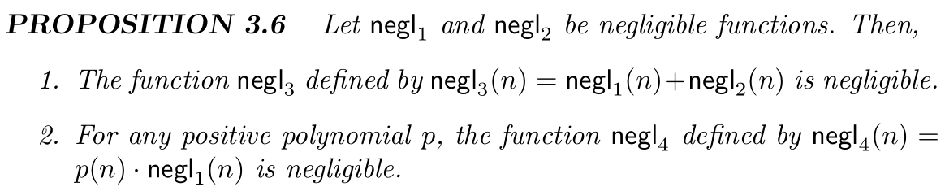
特别的关于推论(2)其暗含了下列事实,如果在一个实验中,某一确定的事件以一个可忽略的概率发生,那么这个实验任意重复多项式时间次,该事件发生的概率仍为一个可忽略的量。
举一个例子,我们来考虑投掷一个公平的硬币(每次实验基本事件发生的概率都相等,为 $\frac{1}{2}$ )这个实验,假设我们投掷这个硬币 $n$ 次,并且每一次投掷的结果都为正面朝上,那么该事件发生的概率为 $2^{-n}$ 是一个可忽略的量,这意味着当我们重复这个实验任意多项式时间次,在这些实验中出现 $n$ 枚硬币同时正面朝上的概率仍然是一个可忽略的量。
总结一下,使用 Asymptotic Approach 对密码方案安全性进行定义规避了在 Concrete Approach 中面临的困难,使得我们能够将具体的密码方案安全性抽象出来用以进行理论分析,现在我们可以提供一个完整的定义,

可以看到我们对攻击者的能力(算力/时间资源)进行了约束,并且通过引入安全参数 $n$ 我们可以控制密码方案的安全性,能够从理论上观察随着安全参数 $n$ 的增加,攻击者所使用的算法在解决它自己的问题上所花费时间的增长趋势,以更好使用这种渐进的方式研究密码方案安全性。可以看到在对于攻击者使用的任意 PPT 算法都有一个确保密码方案安全的阈值 $N$,若安全参数 $n$ 的设置是小于 $N$ 的,这时候攻击者成功的概率就变得不可接受,这时我们可能会说该密码方案是不安全的。值得注意的是,我们在定义一个密码方案的安全性时定义了一个密码方案何时能够被称为“已经被攻破”,并且指定了攻击者所拥有的能力,这些约束使得我们后续讨论攻击者成功的概率具有了意义。
Necessity of the Relaxations
前面我们提到为了能够使安全性定义能够指导我们构造符合生产应用需求的密码方案,我们必须弱化完善保密理论的安全性定义,以便去规避其缺点(我们想要使用短密钥去加密长消息)。我们对完善保密理论定义做出了两方面的弱化:(1)限制攻击者的能力,我们现在只考虑 efficient adversaries 而不像是在完善保密中的一样考虑拥有无限计算资源与无穷时间的攻击者,这样的 relaxation 更加靠近现实中攻击者的能力。(2)我们允许密码方案以一个极小的概率被攻击者攻破,这意味着攻击者存在从密文中获得明文信息的可能性,而在完善保密理论中这种情况是不被允许的。这样我们便可以得到一个安全性相对完善保密弱化但具有实践应用意义的密码方案安全性定义—— Computational Security.
考虑一个加密方案,其明文空间 $M$ 大于其密钥空间 $K$,通过在 Perfect Secrecy 中的学习我们知道这样的方案是不满足完善保密理论的。这时我们假设给定一个密文 $c$,我们使用所有可能的密钥去解密该密文 $c$,得到 $M(c)=\{m| m=Dec_k(c)\space for\space all\space k\in K\}$,并且我们可以得知 $|M|>|M(c)|$,这样我们便泄露了密文中蕴含的明文信息。($M(c)$ 中的元素并不包含所有 $M$ 中的元素,我们得到的结果可能会发现该 $c$ 解密后得到的 $m=Dec_k(c)$ 不在 $M$ 中,对于攻击者来说它能够从其中推测出有关明文的信息)。
为了直观的说明这些定义上的弱化所带来的结果,我们考察教材上的一个例子,
考虑已知明文攻击:$c_1,c_2,c_3,…,c_l$ 是明文 $m_1,m_2,m_3,…,m_l$ 加密后得到的密文。作为攻击者,我们现在又两种攻击路线,
- Exhaustive-search attack 穷尽搜索攻击
对于每一个密文 $c_i$ 来说,攻击者可以穷尽密钥空间,找到到一个 $k$ 使得 $Dec_k(c_i)=m_i$ ,我们可以推测这样的 $k$ 大概率就是加密所使用的 $k$,这样当攻击者截获到新的密文 $c^{*}$ 时,其可以使用前面得到的 $k$ 解密密文,得到 $Dec_k(c^{*})=m^{*}$ ,这样我们便可以说改密码方案被攻破了。这种 Exhaustive-search 简单粗暴,在密文空间有限的情况下十分有效,其搜索过程是一个线性遍历的过程,其算法的时间复杂度为 $O(|K|)$,攻击者成功找到密钥 $k$ 的概率接近于 $1$
- Random guessing 随机猜测
对于另外一种攻击路线来说,攻击者通过随机挑选密钥空间中的元素作为其解密密钥 $k\in\ K$ ,若攻击者观察到 $Dec_k(c_i)=m_i$ ,对于所有的 $i$ 都成立,那么其可以认定该密钥空间中的元素 $k$ 就为通信方使用的密钥 $k$ ,这样攻击者就能够使用该密钥 $k$ 去解密后续监听到的密文,解密出明文信息。在这里攻击者是在密钥空间中随机挑选一个元素,其成功的概率为 $\frac{1}{|K|}$,算法复杂度为 $O(1)$.
上述情况我们可以通过设置一个足够大的 $|K|$ 使得攻击者在攻击有意义的情况下运行其算法的时间远小于 $|K|$ (攻击者也许需要花费100年的时间才能够穷尽所有可能的密钥 $k$ ),并且使其对密钥猜测成功的概率远远小于 $1/|K|$ 。
Perfect Secrecy 安全性之所以如此之高并不是因为它能够抵抗所有的攻击,在密钥空间较小的情况下符合 Perfect Secrecy 定义的密码方案仍然是不安全的,尤其是在重复使用同一密钥的情况下。我们所说的安全是指在合理大小的密钥空间下,Perfect Secrecy 定义很好的将明文上的概率分布带到了密文中(通过均匀随机的选取 $k$ ),这也意味着加密操作不会改变原文的概率分布,对于攻击者而言其看到的似乎是另外一种意义下的明文,其概率分布完全独立($Pr[M=m|C=c]=Pr[M=m]$),攻击者无法从密文中恢复出任何有关于明文的信息,这也就是我们所说的 Perfect Secrecy。
Defining Computationally Secure Encryption
经过上述铺垫,我们可以给出一个符合计算安全性的非对称加密方案的定义了,这个定义类似于我们在 Perfect Secrecy 中提到的,不过有一点稍微不同的是我们在这引入了安全参数 $n$ 用以参数化我们的密码方案,使其能够运用渐进的方式分析其安全性,在教材中我们可以得到如下定义:

It is required that for every $n$ , every key $k$ output by $Gen(1^n)$ , and every $m\in {0,1}^*$ , it holds that $Dec_k(Enc_k(m))=m$. If $(Gen,Enc,Dec)$ is such that for $k$ output by $Gen(1^n)$ , algorithm $Enc_k$ is only defined for message $m\in {0,1}^{l(n)}$ , then we say that $(Gen,Enc,Dec)$ is a fixed-length private-key encryption scheme for message of length $l(n)$ .
我愿意将 $Dec_k(Enc_k(m))=m$ 这个条件称为加密语义合理性条件,毕竟对于相同的 $k$ 解密后得到的东西不是原来进行加密的东西,那么也就破坏了加密这个词所包含的语义,在固有印象中加密应该是可逆的过程。在给定了 $k$ 之后 $Enc_k$ 也就变成了一元函数,$m$ 作为其定义域也是自然而然。我们可以看到这里 $m$ 使用比特串进行表示的,并且比特长度(一个关于安全参数 $n$ 的函数)被固定了,我们后续会讨论能够加密任意长消息的加密方案定义。
The Basic Definition of Security (EAV-Security)
在本章节中,我们将讨论最基本的安全定义—— EAV-Security,也叫做窃听者安全,指的是攻击者能够窃听通信双方所使用的信道,能够且仅能够获取一条由特定密钥加密的密文消息,这个时候攻击者无法从该密文中恢复部分明文信息,这时我们就可以说通信双方所使用的加密方案满足 EAV-Security。
正如我们在上一章中所讨论到的一样,任何一个安全定义都由两部分组成:(1)威胁模型(该威胁模型定义了攻击者的能力)(2)安全目标(加密方案所承诺提供的安全能力,这通常表现为该方案在何种情况下可以被认定为“被攻破”)。在 EAV-Security 中我们的威胁模型正是 EAV 假设,我们限定了攻击者的能力(攻击者仅能够从合法主体的通信信道中获取之多一条密文信息并且在 PPT 内运行其攻击算法),与在 Perfect Secrecy Encryption Scheme 中的定义不同,这里的攻击者被限制在 PPT 内运行其攻击算法。通过上述假设,我们涵盖了所有运行在计算能力约束下的 PPT 攻击者,并且不需要考虑它们具体的攻击策略,这意味着我们的加密方案的安全性定义对所有符合算力限制的攻击者都有效,这便是一个有效的威胁模型定义。
而关于安全性目标的具体定义就没有威胁模型的定义那么直观,不过,我们仍能够从其背后的思想获得直观的理解,即攻击者不能够从密文中获取关于明文的部分信息。Semantic Security 给出了该直白表述的公式化表达,不过它较为复杂并且难于理解,不过我们回想起在 Perfect Secercy Encryption Scheme 中提到的 indistinguishability ,我们还是有简单的办法表述该定义。
在后面的学习中我们可以发现 Semantic Security 与 Indistinguishability 其实是等价的。
在给出使用实验交互的方式给出攻击者不可区分的定义前,我们先来看看这里的不可区分性与在 Perfect Secrecy 中学习到的有什么不同。
- 在 Perfect Secrecy 中我们没有对攻击者的能力进行限制,攻击者可以使用无限的计算资源并且允许其运行任意长的时间。而在 EAV-Security 的定义中,攻击者被限制为 PPT 的攻击者,这意味着其运行算法的时间是有限的,并且其所拥有的算力资源也被限制在当代能提供的最大算力资源。
- 在 Perfect Secrecy 中我们在定义不可区分性时要求攻击者进行不可区分性实验时成功的概率精确的等于 $\frac{1}{2}$ ,而在 EAV-Security 中我们运行攻击者实验成功的概率可以大于 $\frac{1}{2}+negl(n)$ 。
- 我们使用不可区分性实验定义 EAV- Security 时引入了安全参数 $n$,这使得我们能够通过“伸缩”安全参数 $n$ 来改变加密方案提供的安全性,这使得我们能够观察每一个 PPT 的攻击者在何种安全参数下其攻破加密方案的概率达到我们的安全性目标。
- 在 EAV-Security 中我们要求敌手 $A$ 输出的明文消息 $m_0,m_1$ 具有相同的长度 $l(n)$ 。我们在 Perfect Secrecy 的不可区分性实验中的定义暗含了明文空间包含了一些固定长度的消息,这意味着我们默认一个安全的加密方案不需要去隐藏明文的长度。
下面我们给出对于一个 private-key encryption scheme $\Pi = (Gen,Enc,Dec)$ ,一个具备 EAV 能力的敌手 $A$ ,和一个安全参数 $n$ 的敌手不可区分性实验 $PrivK^{eav}_{A,\Pi}(n)$ 的定义,
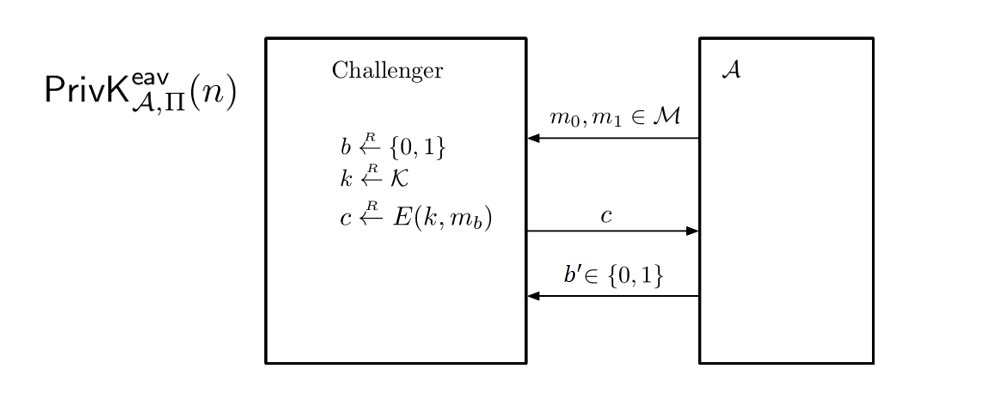
下面我们给出满足 EAV-Security 的加密方案其 adversarial indistinguishability experiment 应该满足下式,

上述定义从攻击者的视角出发,对于每一个 PPT 攻击者,不管它们看到的挑战密文是由 $m_1$ 还是由 $m_2$ 加密而来,它们最终决定输出的 $b'$ 都具有相同行为表现。换句话说,当攻击者接收到挑战密文时它们选择输出 $0$ 还是选择输出 $1$ 与它们看到的密文无关(攻击者根本无法从挑战密文中区分出其到底是由哪一个明文加密而来),因此这些攻击者相当于在 $0,1$ 之间均匀随机的选取 $b'\gets{0,1}$ (也就是乱猜)。
在教材中有提到披露明文长度对加密安全性可能带来的风险,在此便不再赘述,有兴趣的同学可以参考(PG.56)
*Semantic Security
在本章节中,我们将介绍语义安全,语义安全是 Indistinguishability 的另外一种等价表述,它将我们对加密的安全性定义精确地公式化,我们可以看到在这种方式下的定义更加精细能够加深我们对于组成安全性定义各部件的理解。在给出 Semantic Security 的定义之前,我们先来看看两种较弱的表述,并且我们将说明它们暗含了 EAV-Security 的内涵。
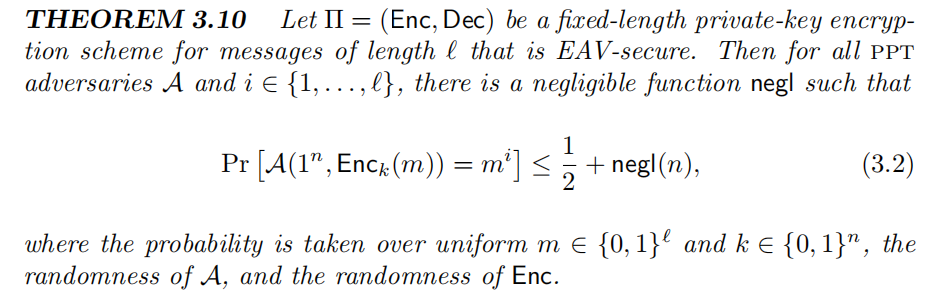
Formally, we show that if an EAV-secure encryption scheme $(Enc,Dec)$ is used to encrypt a uniform message $m\in {0,1}^l$,then for any $i$ it is infeasible for an attacker given the ciphertext to guess the $i$th bit of $m$ (here denoted by $m^i$) with probability much better than $\frac{1}{2}$
在安全参数 $n$ 下,PPT 攻击者无法在观察到密文的情况下能以比 $\frac{1}{2} + negl(n)$ 更大的概率猜测出原文在第 $i$ 位上的比特是 $0$ 还是 $1$ 。在教材(PG.57)中给出了证明,教材在这里使用了 Reduction 证明方式,这样的证明方式在本课程中还会出现非常多次,因此其重要性不言而喻,建议同学们充分理解该处的内容。我将在下方尽可能地讲解该证明的精髓,仅供参考。
为了证明:当 $\Pi = (Enc,Dec)$ 是一个 fixed-length private-key encryption scheme 对长度为 $l$ 的消息是 EAV-Security 的,那么对于任意 PPT 攻击者 $A$ 和 消息中的任意比特位 $i\in {1,…,l}$,存在一个可忽略的函数 $negl$ 有 $Pr[A(1^n,Enc_k(m))=m^i]\leq\frac{1}{2}+negl(n)$ 成立,我们需要对问题进行转换以便利用到方案 $\Pi$ 满足 EAV-Security。也就是说我们可以利用方案 $\Pi$ 满足 EAV-Security 的定义,那么对于任意 PPT 的攻击者 $A'$ ,其进行 adversarial indistinguishability experiment 有 $Pr[PrivK^{eav}_{A',\Pi}(n)=1]\leq\frac{1}{2}+negl(n)$ ,这里我们很容易观察到不等式右边的形式已经相同了,我们需要做的就是利用 $A$ 的能力帮助 $A'$ 去完成它的实验,而 $A$ 的能力就是在给出密文的情况下判断明文某一比特位上的值是 $0$ 还是 $1$ 。回想一下我们在构造 adversarial indistinguishability experiment 时,敌手 $A'$ 在收到挑战密文的情况下需要给出其 $output\space b'$ ,那么在如今的情况下,我们可以让 $A'$ 直接使用 $A$ 的能力帮助其作出判断,注意到 $A'$ 的任务是区分挑战密文到底是由 $m_0$ 还是由 $m_1$ 加密而来的。为了充分利用到 $A$ 的能力,我们可以按照某一比特位具体的值来区分定义 $m_0$ 和 $m_1$ ,具体的构造在教材中由详细说明。这样在 $A'$ 收到挑战密文后,其可以直接把问题丢给 $A$ 去解决,当 $A$ 输出 $0$ 时(也就是 $A$ 认为挑战密文应该是由 $ith$ 比特为 $0$ 的明文加密的,该论断的正确性取决于 $A$ 的能力) $A'$ 也输出 $0$ ,当 $A$ 输出 $1$ 时也同理。这样我们便可以得到
$$Pr[PrivK^{eav}{A',\Pi}(n)=1]=\frac{1}{2}·\mathop{Pr}\limits{m_0\gets I_0}[A(1^n,Enc_k(m_0))=0]+\frac{1}{2}·\mathop{Pr}\limits_{m_1\gets I_1}[A(1^n,Enc_k(m_1))=1]$$
并且,
$$\frac{1}{2}·\mathop{Pr}\limits_{m_0\gets I_0}[A(1^n,Enc_k(m_0))=0]+\frac{1}{2}·\mathop{Pr}\limits_{m_1\gets I_1}[A(1^n,Enc_k(m_1))=1]=Pr[A(1^n,Enc_k(m))=m^i]$$
最终可得,
$$Pr[A(1^n,Enc_k(m))=m^i]\leq\frac{1}{2}+negl(n)$$
我们成功的利用了 $A$ 的能力去解决 $A'$ 的问题并且由于 $\Pi$ 满足 EAV-Security,$A$ 在实验中表现不佳这也导致了 $A'$ 的能力“不足”,我们也可以使用反证法对此进行证明,用 $A$ “强大”的能力去帮助 $A'$ 完成它的任务使其违反 EAV-Security 的定义,从而推出矛盾。
下面我们来看另外一种 EAV-Security 所蕴含的表述,

这里比较晦涩的是这个 $f(m)$ 的出现,我们暂且可以把他看作是将明文进行分类的区分器(比较它将所有明文映射到 ${0,1}$ 上,这么看也是挺自然的),简单理解就是攻击者 $A$ 在获得密文的情况下与没有获得密文的情况下对 $f$ 的构造都是等价的,也就是说运用这个区分器 $f$ 到 adversarial indistinguishability experiment 上帮助 $A'$ 解决它的区分问题不会破坏 EAV-Security 的定义,这个定义是我们上述提到的第二种等价定义。这里又回到了我们最初的目标,攻击者无法从密文中获得有关明文的部分信息。
我们现在能够给出 Semantic Security 的定义了,

直观上理解该定义,密文 $Enc_k(m)$ 没有泄漏任何有关如何高效构造 $f(m)$(没有从密文中泄露有关明文的部分信息) 的信息除了明文的长度 $|m|$ 。$h(m)$ 是有关 $m$ 的一些外部信息,攻击者可以从其它途径(非观察密文)得到。注意 $A'$ 运行着一个 $Samp$ 算法,该算法从任意的明文概率分布空间中选取明文。对 $A$ 来说其拥有密文 $Enc_k(m)$ 与任意外部信息 $h(m)$,其构造区分器的能力与在具有任意概率分布的明文空间上构造区分器的行为不可区分,这也就说明了即使将密文和外部信息为 $A$ 所知,其对如何能构造能够胜任 adversarial Indistinguishability experiment 的区分器仍然无能为力(相当于胡乱构造)。再次强调我们的目标,在 Computational Security 定义下,观察到密文不会泄露有关明文的部分信息。
下列定理说明了 EAV-Secure 的加密方案 $\Pi$,其在 Indistinguiability 与 Semantic Security 上的定义是等价的。


